Quantum state tomography of large nuclear spins in a semiconductor quantum well: Optimal robustness against errors as quantified by condition numbers
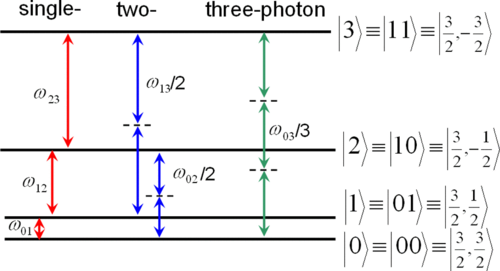
We discuss methods of quantum state tomography for solid-state systems with a large nuclear spin I=3/2 in nanometer-scale semiconductors devices based on a quantum well. Due to quadrupolar interactions, the Zeeman levels of these nuclear-spin devices become nonequidistant, forming a controllable four-level quantum system (known as quartit or ququart). The occupation of these levels can be selectively and coherently manipulated by multiphoton transitions using the techniques of nuclear magnetic resonance (NMR) [Yusa et al., Nature (London) 434, 1001 (2005)]. These methods are based on an unconventional approach to NMR, where the longitudinal magnetization Mz is directly measured. This is in contrast to the standard NMR experiments and tomographic methods, where the transverse magnetization Mxy is detected. The robustness against errors in the measured data is analyzed by using the condition number based on the spectral norm. We propose several methods with optimized sets of rotations yielding the highest robustness against errors, as described by the condition number equal to 1, assuming an ideal experimental detection. This robustness is only slightly deteriorated, as given by the condition number equal to 1.05, for a more realistic “noisy” Mz detection based on the standard cyclically ordered phase sequence (CYCLOPS) method.