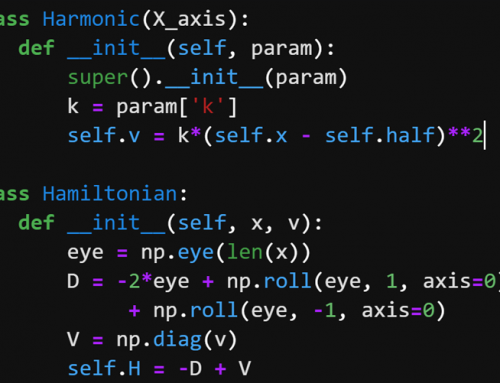
3.2. 二階の常微分方程式¶
二階のODEを解くには、二元連立一階微分方程式に置き換えてやればいい。具体例でみてみよう。
(例題) $\ddot{x} + \dot{x} + x = 0$を、初期値$x(0)=0$、$\dot{x}(0)=1$で解き、$0 \leq t \leq 10$で図示せよ。
まずはmoduleのimport。
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
$x$を位置だと見立てて、時間微分を速度$\dot{x}=v$とすれば、与えられた二階のODEは、以下のような二元連立一階ODEに直せる。
\left \{
\begin{array}{}
\dot{x} = v\\
\dot{v} = -v -x
\end{array}
\right.
\end{equation*}
odeintでは位置$x$と速度$v$が連結された配列が求められるので、この配列をxvとする。xvの$0$列目が$x$、1列目が$v$に対応することになる。これを念頭に連立方程式をfunction fで表す。
def f(xv, t):
f = np.array([xv[1], -xv[1] - xv[0]])
return f
初期値をxv0として、xv0の0番目と1番目の要素をそれぞれ$x=0, v=1$とする。tも定義する。
xv0 = np.array([0, 1])
t = np.arange(0, 10.1, 0.1)
最後にodeintでxvを求めて図示する。
xv = odeint(f, xv0, t)
plt.plot(t, xv)
plt.xlabel("t")
plt.ylabel("x")
plt.legend(["x",'v']);
fを定義したときに説明したように、配列xvの0列目が$x$, 1列目は$v$なので、plt.plot(t,xv)と書くだけで、$x$と$v$を同時にプロットできる。以上のように、$n$階のODEは$n$元連立1階のODEに直せばodeintを使って解くことができる。ODE solverはodeintだけではなくいくつか存在するが、それらについてはSciPyの公式を参照してほしい。
練習問題¶
(3.2.1.) 以下の$I$に関するODE
L\frac{d^2 I}{dt^2}+R\frac{dI}{dt}+\frac{I}{C} = 0
\end{equation*}
を考える。ただし、$L=1, C=1$とし、$R$は下記のような三つの条件とする。
(i) $R = 0.2$
(ii) $R = 2$
(iii) $R = 20$
各条件のもと、初期値$I(0)=1$、$\left.\frac{dI}{dt}\right|_{0}=0$でODEを解き、$0 \leq t \leq 40$で$I$を図示せよ。
解答例¶
(3.2.1.) これはRLC回路の回路方程式である。二元連立ODEに直すと、
\left \{
\begin{array}{}
\dot{I} = v\\
\dot{v} = -\frac{R}{L} v – \frac{I}{LC}
\end{array}
\right.
\end{equation*}
これをコードに直せばよい。上の例でxvと定義してた配列を、の代わりにIvという名前の変数にして、$0$列目を$I$、$1$列目を$v$に対応させる。
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
L, C = 1, 1
r = {0.2, 2,20}
def f(Iv, t):
f = np.array([Iv[1], -R/L*Iv[1] - Iv[0]/(C*L)])
return f
Iv0 = np.array([1, 0])
t = np.arange(0, 40.1, 0.01)
for R in r:
Iv = odeint(f, Iv0, t)
plt.plot(t, Iv[:,0])
plt.legend(r)
plt.xlabel('$t$')
plt.ylabel('$I$');
微分方程式のところで勉強したと思うのだが、$\alpha = \left( \frac{R}{2L} \right)^2 – \frac{1}{LC}$によってODEの解の振る舞いは異なる。(i)のように$\alpha$が負だと解は振動し(振動減衰)、(ii)$\alpha=0$のとき最も早く減衰する(臨界減衰)。(iii)のように$\alpha$が正になると過減衰といって減衰が遅くなる。RLC回路を流れる電流は、摩擦のあるばねの振動(例えば粘性液体の中においたばね)の変位を表す微分方程式と同じなので、(i)の時は粘性(抵抗)が強くないため、ばねは振動減衰しながら自然長の位置に戻る。(ii)の条件では振動せずに最も速く自然長の位置に戻る。(iii)では粘性(抵抗)が高すぎるので、なかなか自然長の位置に戻らないということと等価である。
当サイトのテキスト・画像の無断転載・複製を固く禁じます。
Unauthorized copying and replication of the contents of this site, text and images are strictly prohibited.
© 2019 Go Yusa